ロジスティックス方程式の対角化解法
以下にロジスティックス方程式
![]()
を対角化解法によって解くことを行なう。この方程式は代表的な非線形微分方程式の一つである。
この方程式の解は
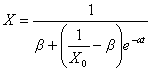
であることが一般に知られている。つまりここでは、対角化解法によってもこれと全く同じものが求められることを示すわけである。
この方程式は、例えばある量が成長していく過程で次第にその成長を阻害する要因に遭遇して、その抵抗で成長が鈍化していくなどという局面に用いられるものであり、それゆえその曲線は成長曲線とも呼ばれている。そしてこの場合重要なのは、これまでの対角化解法で扱ってきたものが線形方程式であるのと違って、これが非線形方程式であるということである。あらためて言うまでもないことではあるが、従来の微分方程式論においては、線形方程式については基本的にそのほとんどが解明されているが、非線形方程式というものは、いまだその体系の全体像がつかめていない一種の暗黒領域である。そのためこの方程式を対角化解法で解くことは、われわれの体系が新たな領域へ一歩踏み出すことを意味すると言ってよいだろう。そして一般に作用マトリックスn乗理論では、非線形問題の扱いに際してスイッチ演算子の概念が決定的な役割を果たしているが、この場合もやはりスイッチ演算子が重要な役割を担っている。しかしそれならこれが初学者には縁のない高級な贅沢品なのかといえば、必ずしもそうとは言えず、実は意外にもこれはもっと基礎的な問題に関しても重要な土台になるものと考えられる。それというのも例えば微分方程式では、いわゆる変数分離型の方程式などは一般には最も初歩的なものと考えられているが、これを対角化解法で解こうとすると意外なほど難しい。ところがそれは、このロジスティックス方程式に関する結果の一部を利用することで解法が得られ、逆に言えばそれはこの非線形方程式を一旦経由しないことには、容易に解決方法が見つからないという性格のものだったのである。つまり非線形問題とは言いながらも、この解法の考え方は対角化解法全体においてかなり基本的な位置を占めてしまうことになると予想されるわけであり、それゆえその点をご了承されたい。
さて、このロジスティックス方程式の場合、第二項が2乗を表わす非線形項となっており、この部分はスイッチ演算子によって表現する必要がある。そしてそれをどう表現するかの基本思想については、この方程式の原点に立ち返ればよい。すなわち先ほど述べたように、基本的にこの方程式は、Xという量が成長していく際に、その途上でさまざまな成長阻害要因に遭遇してその成長速度がだんだん鈍っていくことを示すものであると解釈される。そしてこの場合、自身のサイズが大きくなればなるほど、新たな成長阻害要因に遭遇する確率が増大し、それがサイズXに比例すると考える。


そしてこれをスイッチ演算子で表現する場合、Xの値が大きくなっていくにつれて、階段状に次々と新たな阻害要因に接触していくと考え、その瞬間において次々にスイッチ演算子が作動していくと考える。そしてその中間の期間は線形方程式として考えられることになる。
では具体的にはどういう形で作用マトリックスの中に組み込まれるのだろうか。それは、まず列ベクトルの一番上に各時点でのXの値が表示されるようにしておき、その下に、各阻害要因を並べていき、それへの接触状況R1、R2、・・・Rk・・が列ベクトルの中に表示されるようにしていく。そして各阻害要因との接触がそれぞれX = X1、X2、・・Xk・・の時点で起こるとすれば、スイッチ演算子S(Xk)を作用マトリックスの左端の列に並べ、また各阻害要因が単位接触あたりに及ぼす抵抗率をβkとしたとき、それを作用マトリックスの一番上の行に並べる。すなわち
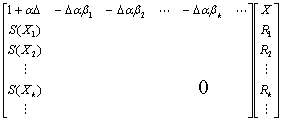
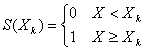
という形になる。このようにすると、Xの値が大きくなるにつれて次々に新たな阻害要因に接触し、平均的に見るとX2で抵抗値が大きくなっていく状況が表現されることになる。
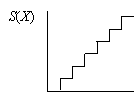
一般にはβkの値はそれぞれ異なるはずであるが、これをすべて等しくβk=βと仮定し、また各Xkの値が等間隔であると仮定して極限をとると、ロジスティックス方程式に移行する。なおこの条件が仮定されている場合、上記のような表現法が煩瑣で不便ならば、もう少し簡略化された表記も可能である。すなわちスイッチ演算子sのかわりに階段関数Sを考えて
![]()
X
としてやっても一応は表現が可能である。
ロジスティックス方程式のマトリックス解法
では作用マトリックスとスイッチ演算子の組合せを用いても、解析的に解いた場合と同様の解が求められることを、以下に示そう。
具体的にはそれは次のような考え方を用いて行う。すなわち、系の時間的な変動を、スイッチ演算子の作動点ごとに切れ目を入れてそこで分割し、分割された個々の部分は線形系として取り扱う。そして最後にそれをつなげていく。
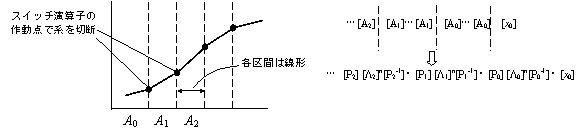
このため、実はここには一つの条件が暗黙のうちに仮定されている。つまり系を差分化して作用マトリックスを設定する場合の時間分割の規模は、スイッチ演算子の作動による分割の規模よりも遥かに細かくできるという条件である。(実際そうでないと、スイッチ演算子の作動点の間をさらに作用マトリックスのn乗で表わすということができなくなってしまう。)これは、スイッチ演算子の本来の思想からする限り何ら無理な仮定ではなく、実際に現実の非線形系では、この条件を想定できる場合の方がむしろ多いものと考えられる。(そうでない場合への拡張については、後にあらためて議論する。)
このように切断した小区間作用マトリックスをそれぞれA0、A1、A2・・・とした場合、それは先ほどの作用マトリックスのスイッチ演算子の部分をゼロか1にしたものになる。すなわちA0はすべてのスイッチ演算子がゼロ、A1は最初の1個だけが1、そして次々にゼロが1に変わっていくことになる。
0 0 0

そしてこれらを全部対角化して最後につなげてしまえば良いわけだが、最初のA0についてはその固有値が1+aDであることは自明であるが、次のA1について見てみよう。(この場合、行列サイズが大きいと記述が面倒なので、3×3に落として調べる。)
作用マトリックス

の固有値は
![]()
であるが、D→0で平方根を展開して、結局対角行列L1は
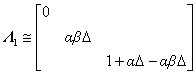
と近似できることになる。また変換行列Pの方は、やはり近似により
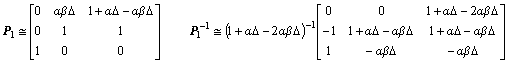
となり、A1の対角化それ自体は
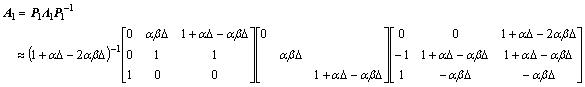
という形になる。そしてこれをn乗することを考えると、もう一段の近似が可能となる。
すなわちL1のn乗の側が
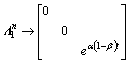
になるのは言うまでもないが、Pの側には最初の仮定が効いてくる。すなわち最終的にこれらを接続する場合、
![]()
となるが、この中に含まれるLiとPiおよびPi-1の個数を考えると、
![]()
と考えてよいことになる。そのためPiおよびPi-1の中に含まれる1+Dなどは実は→1としても差し支えなくなるのである。
つまり最終的にA1の対角化は
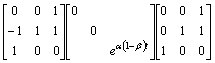
と近似できる。
同様にAkに関しては
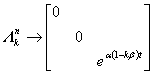
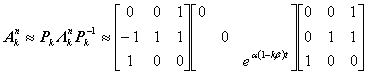
とできることになり、結局単純にexpa(1-kb)tをつなげていけば良いことがわかる。
注) 今の例は一番基本に忠実に行った場合だが、最終的な結果は簡略化した形式によっても得ることができる。すなわち先ほどのように最初の作用マトリックスを
![]()
としてやれば、
![]()
と対角化でき、expの中身だけが段階的に変化していくという基本的な構図は同様にして浮かび上がってくることになる。
さて切断した各小区間作用マトリックスが基本的にexp(1-kβ)tになることが確認できたので、後はこれをつなげてtとXの関係を求めれば良い。そしてスイッチ演算子の作動点が等間隔であることが仮定されているので、その作業はある意味で、ちょうど通常の場合とはグラフを縦横逆にした格好で関数の形を求めていくようなものとなる。つまり通常の場合、言うまでもないことだが、横軸の側を等間隔の微小区間に区切って各区間でのグラフの高さを求め、それをつなげていくという形で、全体の曲線の姿が求められる。しかしこの場合には、スイッチ演算子の作動点に対応する格好で、むしろ縦軸の側が等間隔に区切られる形で小区間が設定されている。そのため各区間で通常とは逆に横軸方向の幅の方を求め、それをつなげていくというやり方を用いて、全体の曲線の形を求めていくわけである。要するに等間隔に並んだXkに対してその時間間隔dkを求めて、それをつなげることでXとtの関係を求めるということになる。
ではそれを求めていこう。まずdtk = tk - tk-1とすると、各部分で
![]()
より
![]()
ここで
![]()
と置き換えると
![]()
である。そのためtを求めるには単にこれを積分すればよく、
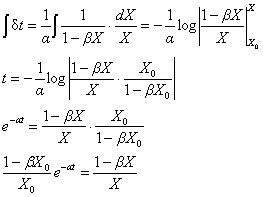
である。つまり最終的に
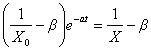 より、
より、 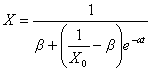
となり、作用マトリックスとスイッチ演算子で記述したものを単純に対角化してつなげるだけでも、一般に知られているロジスティックス方程式の解と同じものが求められることがわかる。なお、今の場合には仮定として、スイッチ演算子の作動による分割が相対的にさほど細かくないということが想定されている。
S,Naganuma,Rep.Path Find.Phys.,Vol.1,pp.54-61(2003)